Improvement of the Wavefront Correction in Adaptive and Active Optics--Purple Mountain Observatory

Improvement of the Wavefront Correction in Adaptive and Active Optics

Optical systems have their own optical aberrations due to their designs and manufacturing errors. The well-known Zernike polynomials, proposed by Frits Zernike, whose orthogonal functions are defined on the unit circle, are widely used to represent the optics aberrations. The optical aberrations can be usually corrected by active optics or adaptive optics. The task of adaptive optics or active optics is to adjust the deformable mirror to compensate the optical aberrations in the most effective way. However, researchers have shown that Zernike polynomials performed somewhat less efficiency over the dynamic range of the aberration corrections of the active optics systems. Moreover, some aberrations represented by the Zernike polynomials are not easy to compensate.

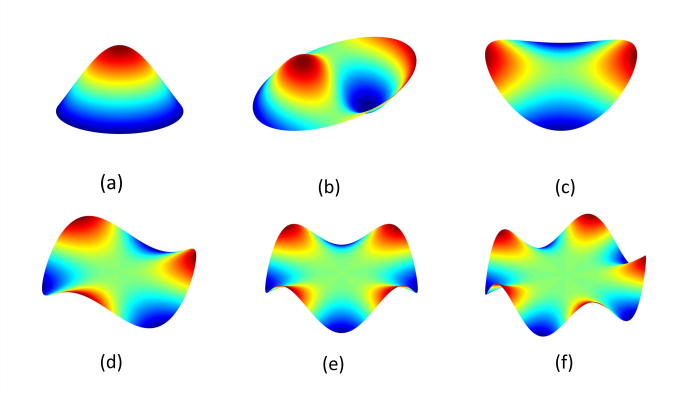
In a recent paper by WANG Hairen et al from Purple Mountain Observatory (PMO) of the Chinese Academy of Sciences (CAS), the elastic modes of a general circular thin plate (EMCTP) are proposed, and they are more easily extended to optics systems instead of the use of the standard Zernike polynomials. In Fig, 1, the mode shapes resemble those of the standard Zernike polynomials are shown, and there is almost a one-to-one match between each resonant mode and each standard Zernike polynomials.

Fig. 1 The mode shapes of the EMCTP. [Image by WANG Hairen]

After applying the EMCTP to the simulations of the aberrations compensations of the active optics systems, a quantitative comparative study of the active optics corrections is presented in Fig. 2 between the EMCTP and the standard Zernike polynomials. The quantitative analysis results have shown that the EMCTP can not only be used instead of both the standard Zernike polynomials and the annular Zernike polynomials, but also be more effective to compensate the aberrations compared to the two kinds of Zernike polynomials.

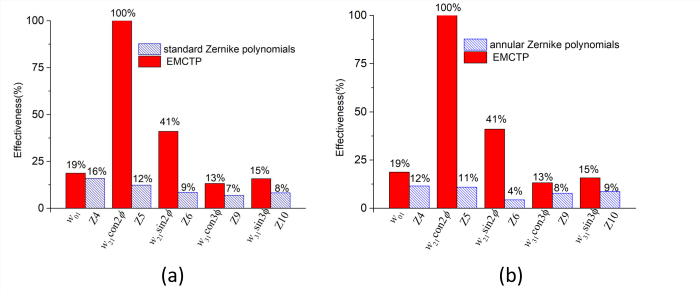
Fig. 2 (a) Comparison between the EMCTP and the Standard Zernike polynomials on effectiveness; (b) Comparison between the EMCTP and the annular Zernike polynomials on effectiveness. [Image by WANG Hairen]

This work has been published in Optics Express, and is supported by the Key Research Program of the Chinese Academy of Sciences, the National Natural Science Foundation of China, and the Youth Innovation Promotion Association CAS.