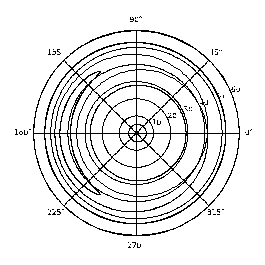
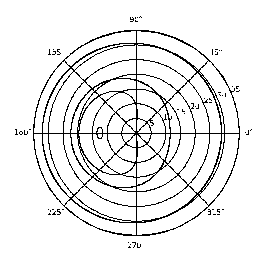
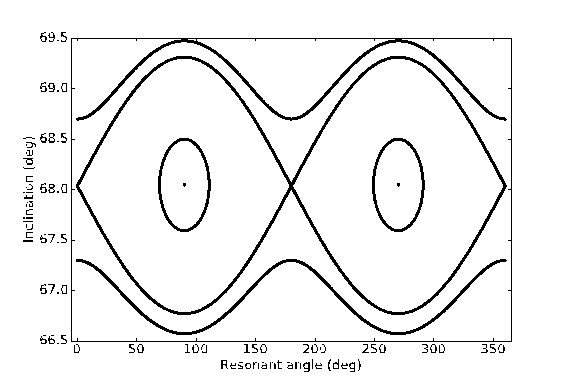
The orbital area of the global navigation satellite system (GNSS) has been very attractive to researchers who work in orbital dynamics, due to the background of complex resonances and chaotic motion. Recently, we developed an analytic model to describe the long-term evolution of GNSS orbits governed by Earth’s J2 and luni-solar gravitational perturbation. The analytic model is accurate compared with numerical results except for the resonant cases, i.e. when the period of the reference orbit approximately equals the integer multiples (especially 1 or 2 times) of lunar node regression period.To resolve the resonant cases, we investigated the lunar node resonance by means of Lie-transformation. The resonant condition is showed in Figure 1. There are two types of phase structures of the 1:1 resonant and showed in Figure 2, with a = 26554 km (left) and a = 29000 km (right) being as two examples. In addition, the 2:1 phase structureisshowed in Figure 3 with a = 26554 km as an example.
|
|
|
|
Figure 1. Phase plane structures of the 1:1 resonance in polar coordinates. Left: a =26554 km, right: a = 29000 km. The radial coordinate is the mean inclination, and the angular coordinate is the resonant angle. |
|
|
|
Figure 2. Phase plane structures of the 2:1 resonance in cartesian coordinates at a = 26554 km. The y-axis value is the mean inclination, and the x-axis is the resonant angle. | This work by Ting-Lei Zhu has been published in Advances in Space Research. Please see Vol.61 No.11 p.2761-2776 for more detail: https://www.sciencedirect.com/science/article/pii/S0273117718302205 |
