The increasing amount of space objects makes the space so crowded that the satellites in orbit endure severe environment. Hence how to efficiently search and catalog these space objects becomes an urgent problem to be solved. In order to contribute to this problem, the secular analytical solution of the orbital plane for medium and high orbit objects is studied. For medium and high orbit objects, the Earth’s oblateness and the lunisolar gravitational perturbations are considered. The double averaging method is used to first average the system. For small to medium orbit inclinations and small eccentricities, and then the differential equations can be rewritten in an expansion form. Combining the Lindstedt-Poincare′ procedure and the solution for differential equations with special coefficients, the third-order analytical solutions can be derived step by step. Finally, two kinds of comparisons are carried out. One is the comparison between the analytical solution and the results derived by integrating the simplified model. It aims to verify the validity of these methods. The other one is the comparison with the integration results of the normal model to show the accuracy of the analytical solution. Both of the two comparisons results work well. The accuracy of the analytical solution can be maintained at the order of O(10^-3) for the duration of 200 yrs.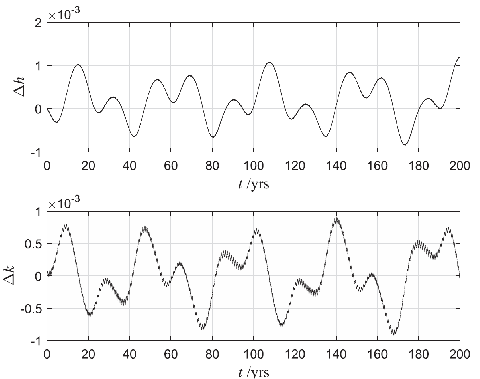

By with Shengxian Yu

Fig. Numerical comparison: the differences of h=sin(i)cos(Omega) and k=sin(i)sin(Omega) between the analytical solution and the results by integrating the normal model.

  This work by Shengxian Yu, Changyin Zhao & Wei Zhang has been published in Advances in Space Research.

  Plese see 60, 10 (2017 2166-2180) for more detail:http://www.sciencedirect.com/science/article/pii/S0273117717306270?via%3Dihub