Type Ia supernovae (SN Ia) have proven useful for measuring cosmic distances.It is understood that their intrinsic luminosity can be standardized, therefore astronomers can estimate their distances by observing how bright they appear to be during the peak of their explosions. In this sense, SN Ia are regarded as "standard candles": the dimmer they appear, the more remote they are from us. The distance so indicated is known as the "luminosity distance" in cosmologists' jargon. The light from distant supernovae are also subject to another observable effect, namely the so-called "redshift", or increase of wavelength, as it propagates through the expanding universe. The relation between redshift and luminosity distance can be sensitive to details of the theoretical model of the universe. 

  For instance, one may attempt to answer the question "Is the cosmic expansion accelerating?" by performing a statistical analysis over a family of cosmological models indexed by several parameters, including the dark matter and dark energy contents of the universe. By requiring the model prediction to fit the observed data, one may narrow down the possible choices of the parameter values and locate the ranges that are mostly likely to explain the observed redshift--distance relation. 

  However, a survey of existing analyses reveals inconsistent application of statistical methods that may lead to biased parameter estimates. For this purpose, we first investigate the theoretical foundation of these methods. We apply the theory of Bayesian graph, a unified description of dependence between random variables, to formalize the process of statistical inference as it ought to be performed in a self-consistent manner. The formal analysis proves helpful in elucidating the source of possible errors that are present in the literature.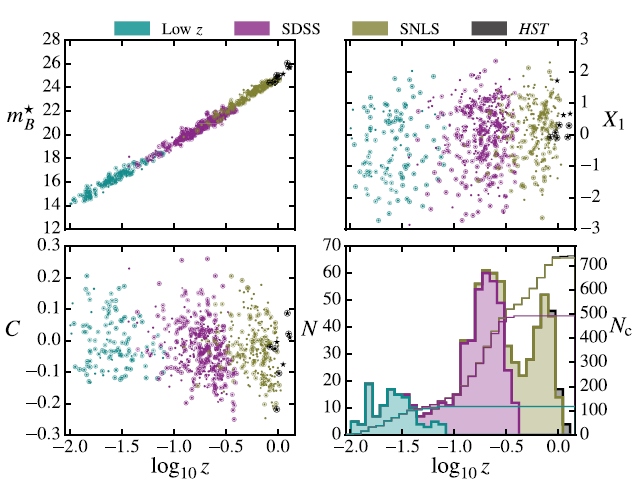 

By with MA Cong

   Fig.Visualization of the JLA data set coloured by the four component source surveys (low z, SDSS, SNLS and HST). Displayed are the apparent peak magnitude m B (top-left panel), the light-curve stretch X1 (top-right panel) and the colour C (bottom-right panel). The bottom-right panel shows the SN redshift empirical distribution (left axis, filled histograms) and the cumulative distribution (right axis, unfilled histograms).

  After that, we also examine the practical ramifications that stem from the mathematical modeling. Two special cases are emphasized, namely parameter  inference and data compression. For the former, we implement Monte Carlo Markov chain analyses to demonstrate the extent of parameter bias (cf. Figure 1). For the latter, we devise a novel technique that reveals the structural and systematic difference in compressed covariance matrices based on the generalized eigenvalue problem. This method also leads to the discovery of a new visualization of covariance matrix differences shown in Figure 2. 

Overall, the analysis presented here stresses the necessity of using self-consistent Bayesian statistical approaches to perform unbiased model parameter inference of SN Ia to generate unbiased sets of compressed data. This work is a collaboration of the Purple Mountain Observatory, the Observatory of Paris--Meudon, France, and University of Cape Town, South Africa. The computer code used for this work is released as open-source software. 

For details, please consult the article "Application of Bayesian graphs to SN Ia data analysis and compression" published in the Monthly Notices of the Royal Astronomical Society, vol. 463, issue 2, pp. 1651--1665 (https://dx.doi.org/10.1093/mnras/stw2069).