The geosynchronous ring is a valuable orbital resource; and there is much uncontrolled space debris in this region. The dynamics of space debris in the geosynchronous ring are complex. The essence of dynamics (i.e., 1:1 orbital resonance and orbital plane precession) drives the motion state and the variation ranges of motion parameters for space debris. The statistical distribution of space debris in the geosynchronous ring is one of the most intuitionistic descriptions of the dynamical phenomenon, which is definitely caused by the essence of dynamics.

   It is important to be certain of the motion state for space debris in the geosynchronous ring and thus quantify the evolution of debris and the risk of a collision. There is no doubt that it is better to use the variation ranges of motion parameters to characterize the evolution of debris quantitatively. Can the motion state and the variation ranges of motion parameters for space debris in the geosynchronous ring be directly determined from only one set of known orbital elements, and can the variation ranges of motion parameters fully illustrate the three-dimensional (3D) variations of space debris?

   Following our previous work (Zhao et al. 2013, 2015), we propose a method that uses only one set of known orbital elements to directly determine the motion state and variation ranges of motion parameters, including the inclination, longitude of the ascending node, evolution period of the orbital plane, maximum libration amplitude of the semi-major axis, commensurable angle, libration period and drift period, for space debris in the geosynchronous ring. The specific determination procedure was elaborated. The motion state and the variation ranges of motion parameters in the two-dimensional (2D) phase plane are dominated by the 1:1 orbital resonance virtually, and the variation ranges of motion parameters in the orbital plane are dominated by the Laplace precession of the orbital plane virtually.

   Employing the proposed method, we study the motion state and variation ranges of motion parameters for all catalogued and uncontrolled space debris in the geosynchronous ring, and present specific results. We also compare our results with actual observational results derived from long-term two-line element (TLE) historical data, and find that, in the vast majority of cases, our proposed method of determining the motion state and the variation ranges of motion parameters for space debris in the geosynchronous ring via only one set of known orbital elements is effective.

   We obtain the statistical distribution of space debris in the orbital plane and the daily motion from the TLE historical data, which both arise from the dynamical way that space debris in the geosynchronous ring precesses around the Laplace plane. We then derive two mathematical formulae that explain the statistical distribution and daily motion on the basis of this essence of dynamics, which contributes to the characterization of the evolution of debris. More importantly, the variation ranges of motion parameters in the orbital plane can often be derived from these statistical distribution characteristics.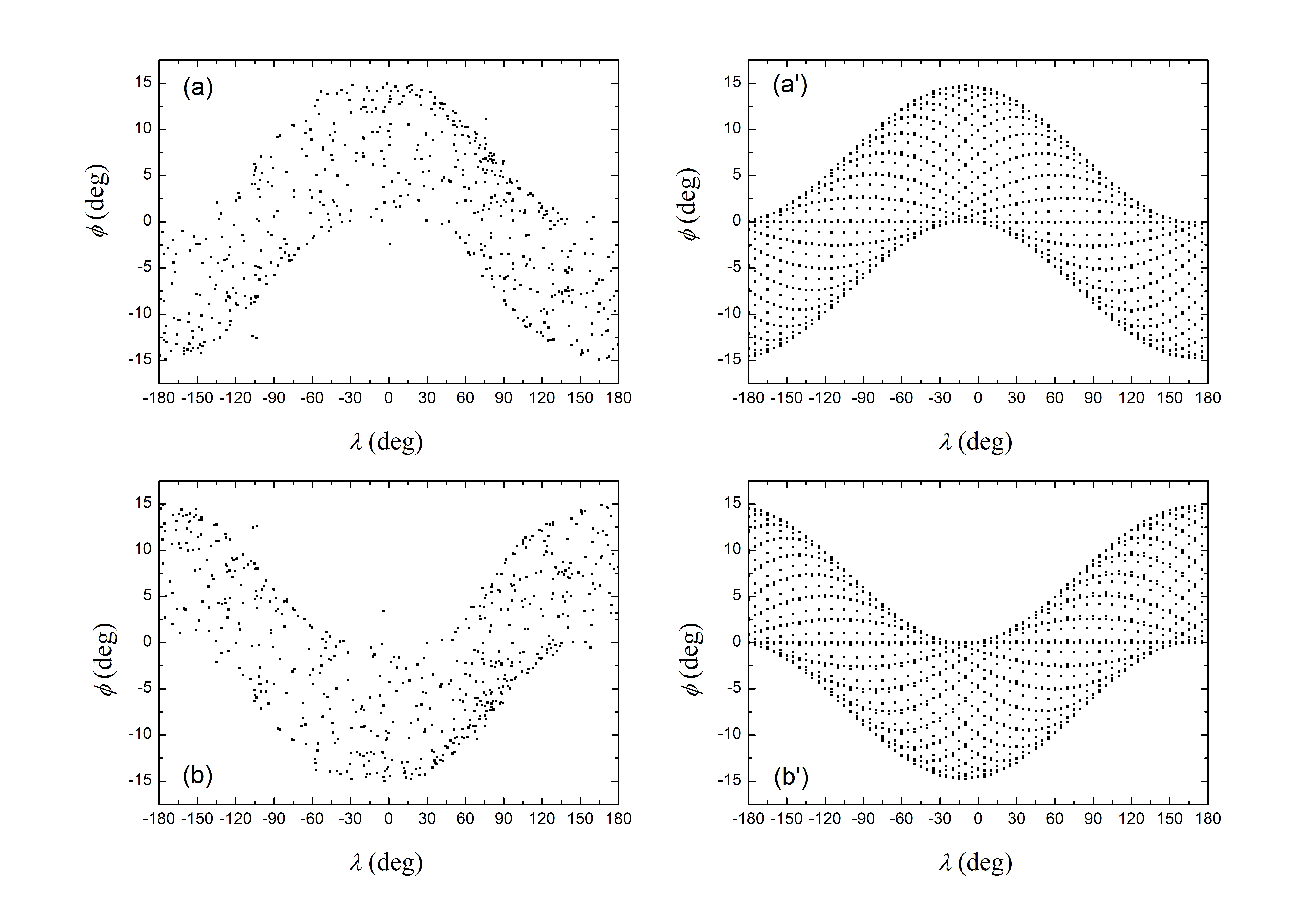

By with ZHAO Changyin

    Fig. 1. The actual and theoretical daily motion of geographic latitude φ and longitude λ of space debris: (a) actual daily motion at the epoch 1 Jan 2014, 00:00:00 UTC, for 568 pieces of space debris; (b) actual daily motion at the epoch 1 Jan 2014, 12:00:00 UTC, for 568 pieces of space debris; (a’) theoretical daily motion at the epoch 1 Jan 2014, 00:00:00 UTC; and (b’) theoretical daily motion at the epoch 1 Jan 2014, 12:00:00 UTC

   The work by Chang-Yin Zhao, Ming-Jiang Zhang, Sheng-Xian Yu, Jian-Ning Xiong, Wei Zhang and Ting-Lei Zhu has been published in Astrophysics and Space Science. Please see the link for more details: http://link.springer.com/article/10.1007/s10509-016-2781-5. This work was supported by the Key Program of the National Natural Science Foundation of China (Grant nos. 11033009 and 11533010) and the National Science Fund for Distinguished Young Scientists of China (Grant no. 11125315).