Newton’s inverse-square law of gravity and Einstein’s general relativity (GR) can explain and describe most of astronomical and astrophysical observations and phenomenon quite well. However, this triumph ceases when they are facing the flat rotation curves of spiral galaxies without introducing dark matter and the present acceleration of the Universe without dark energy. Another way to solve the problems is to modify the theory of gravity and interesting astrophysical and cosmological consequences can be generated by these modified theories. 

  As a generalization of GR, the f(R, T) gravity replace the gravitational Lagrangian of GR with an arbitrary function of the Ricci scalar R and of the trace of the stress-energy tensor T. It can induce an extra acceleration a _E in the dynamics of massive test particles due to the physical coupling between matter and geometry. In current work, some researchers confront this extra acceleration with planetary motions in the solar system. Using the supplementary advances in the perihelia provided by current INPOP10a and EPM2011 ephemerides, they obtain new upper limits on a _E when the uncertainty of the Sun’s quadrupole moment and the Lense-Thirring effect due to the  Sun’s angular momentum are properly taken into account. These two factors were mostly absent in previous works dealing with a _E.  

 The work find that INPOP10a yields the upper limit as a _E=(-0.04±4.81)×10^-15m s^-2 and EPM2011 gives a _E=(0.06±1.58)×10^-15m s^-2 (see the table). Both of them are improved at least by about 10 times than previous results obtained in the solar system and they are smaller than the results given by fitting rotation curves of galaxies by about 4 orders of magnitude. This discrepancy of a _E on these scales seems to imply that its effects might be screened in high density regions.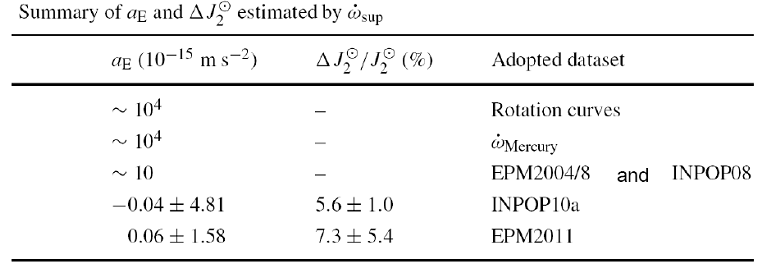 

   This work is done by Dr. Xue-Mei Deng of Purple Mountain Observatory who is collaborated with Dr. Yi Xie of Department of Astronomy in Nanjing University. And this research is supported by the National Nature Science Foundation of China and the National basic research program of China (Nos. 11473072, 1103085 and 11103010) and the Fundamental Research Program of Jiangsu Province of China (Nos. BK20131461 and BK2011553).  For more details, please see the following link: http://link.springer.com/article/10.1007%2Fs10773-014-2377-1