General Relativity has been great at reproducing and predicting phenomena in the Solar System, such as the bending of light by the Sun. However, observational data from supernovae suggest that the expansion of the universe is accelerating and this only be explained in the theory with an additional element. General relativity with a cosmological constant (the so-called ΛCDM-model) is consistent with all current observations - but is plagued by the infamous cosmological constant problem, i.e. nobody can explain the physical nature of this constant.

An alternative is to consider a theory of gravity that reduces to general relativity in the solar system but works differently on cosmological scales, such that it naturally drives the acceleration. In our analysis, we introduce a scalar field that interacts with matter, giving rise to a fifth force that makes matter deviate from their geodesics. Furthermore, the interaction depends on the composition of a massive body, thus allowing for environment-dependent behaviour.

  We can use this environment-dependent, specifically local matter density to allow for deviations from general relativity on large scales while hiding troublesome modifications in the solar system. This is called screening. Two examples of screening mechanisms are the symmetron and the chameleon mechanisms. The symmetron mechanism works by suppressing the coupling of the field to matter in high density regions, i.e. suppressing their interaction; while the chameleon field's effective mass increases somewhere dense, resulting in a very short-ranged fifth force, irrelevant to macroscopic dynamics.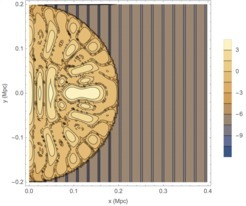

Fig. The relative effect of an incoming scalar wave on the deviation from general relativity in the Milky Way halo (technically: the parameterized post-Newtonian parameter γ.). The wave effectively travels through a medium with a refractive index different from one, similar to light passing through

  Until recently, these screening mechanisms have been studied under the quasi-static approximation. This means that one takes the equation of motion and assumes that the scalar field evolves very slowly. We can then neglect time derivatives and obtain the familiar Poisson-type equation, just like in Newtonian gravity, which does not allow for wave propagation.

See:http://www.mpa-garching.mpg.de/517122/hl201802